Students are often confronted with square roots when being asked to differentiate or integrate functions. Too often, they freak themselves out over not knowing how to deal with the square root instead of simply rewriting it as a fractional power, after which the process becomes identical to differentiating/integrating a normal polynomial function.

Being able to transform an exponential equation into a logarithmic equation (and vice versa) is the most important skill in students' study of logarithms, yet many simply forget this process, and are therefore unable to solve equations where the unknown variable lies in a power.

When evaluating indefinite integrals, it's imperative that students remember to add an arbitrary constant to their answer. However, since this is such a small step, and doesn't actually affect the rest of their answer, students chronically forget this detail, costing them easy marks.

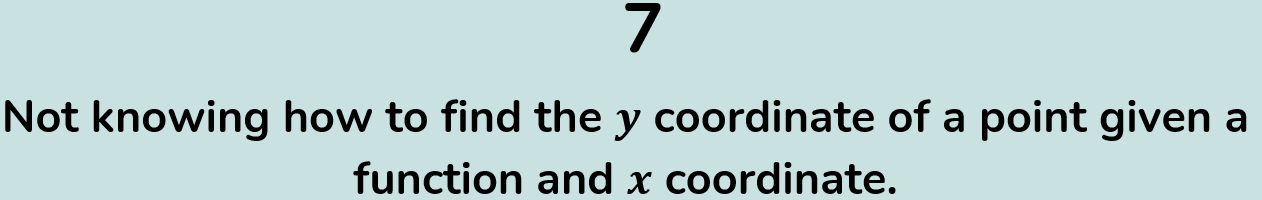
In maths, a "function" is an expression into which if an "x" coordinate of a point is substituted, the "y" value of the same point will be returned. Unfortunately, students often forget that they can use functions in this way, and so frequently find themselves in situations where they are unable to calculate a particular "y" coordinate.

Differentiation is a process with very specific rules. One such rule is that the derivative of the product (or quotient) of two functions must be calculated using the product (or quotient) rule. It is not possible, as students often claim, to simply find the derivatives of the two individual functions and then multiply (or divide) them together.

Although rote learning is all but non-existent in high-school maths, it does show up in trigonometry, whereby students are required to memorise the sine, cosine, and tangent values of five different angles. However, the vast majority of students don't ever actually put in the time to do this, costing them dearly in exams.

Similar to the tenth biggest mistake that we previously mentioned, this mistake relates to students not rewriting particular expressions as powers of the unknown variable when taking derivatives. This one ranks higher than its counterpart because it tends to show up far more often on exams, and is understood by students to a seemingly lesser extent.

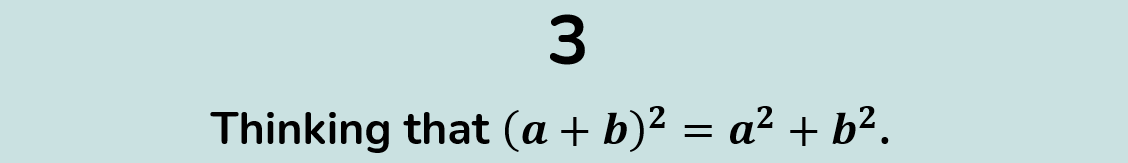
Colloquially known as the "Freshman's Dream", many would rank this as the most egregious mistake made by high-school students. While it doesn't quite top our list, it's certainly close. Despite learning how to expand perfect squares in Year 8 or 9, even senior students consistently make the mistake of thinking that the power of two can simply be "distributed" inside the parentheses when in fact, an additional "cross term" is required in the expansion.

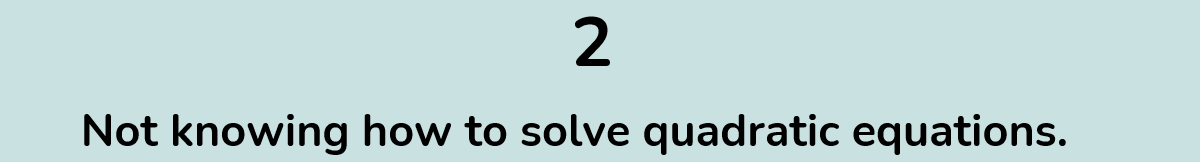
In Year 10, students are taught how to solve quadratic equations. In our opinion, this is the most important skill in high-school maths, because it can easily be incorporated into questions on any topic - calculus, trigonometry, and even probability. However, students generally don't make enough of a point of retaining this skill, and as a result, throughout Year 11 and 12, are frequently unable to progress past the very first step of exam problems that are often worth a significant number of marks.

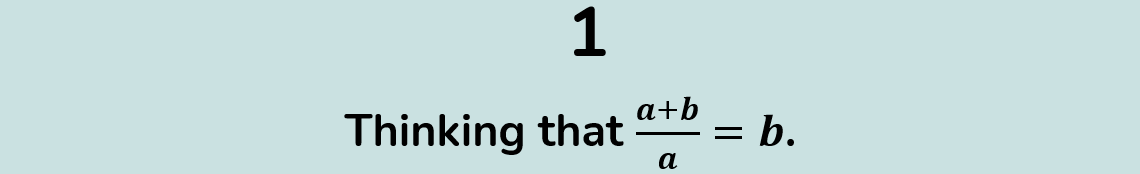
Without a doubt, this mistake takes out the top spot on our list. We call it "cherry-picking". In situations such as the one shown above, students will make statements to the effect of: "I'm just cancelling an "a" off the top and bottom". In reality, they are not doing this at all - they are merely dividing an "a" out of the terms that they want, hence the term "cherry-picking". In reality, dividing "a" out of the top and bottom would involve dividing it out of every term on the top and bottom, which in this case, is not possible, as the "b" term does not contain an "a".

How many of these mistakes have you been guilty of in the past? More to the point, how many of them do you still find yourself making?